 Copyright Sociological Research Online, 1999
Copyright Sociological Research Online, 1999


Brendan Halpin (1999) 'Is Class Changing? A Work-Life History Perspective on the Salariat'
Sociological Research Online, vol. 4, no. 3, <http://www.socresonline.org.uk/4/3/halpin.html>
To cite articles published in Sociological Research Online, please reference the above information and include paragraph numbers if necessary
Received: 26/2/1999 Accepted: 27/9/1999 Published: 30/9/1999

 Abstract
Abstract
- Has the massive transformation of the class structure over the twentieth century changed the consequences of class? In particular, does the fact that the salariat has taken over from the manual working classes as the largest category mean that the implications of membership of the salariat for one's life chances is no longer the same? This paper takes retrospective life-history data from the British Household Panel Study and models patterns of change in the structure of work-life mobility between the ages of 25 and 35 for individuals born between 1900 and 1959. The purpose is to seek evidence of broad changes in the consequences of class, through the middle and late 20th century, using an extremely valuable data resource. The evidence suggests that there is cross-cohort change in the patterns of work-life mobility, both in terms of traditional class categories and in terms of the relationship between class and more general employment status categories, but more strongly in the latter case. In general, the pattern is one of declining immobility, including declining salariat retentiveness. The paper concludes with a consideration of what the data mean, and what this particular bounded analysis has to say about the question of change in the consequences of class.
Keywords:- Class Analysis; Cohort; Employment; Loglinear; Longitudinal; Social Mobility
 Introduction
Introduction
- 1.1
- Is the structure of social class changing? With the huge growth in
white-collar and administrative work in western societies
throughout the second half of the twentieth century, can we
continue to use concepts of class developed in a time when the mass
class was manual? Further, given changes in recent years in the
nature of white-collar employment that many commentators see as a
radical end to the security hitherto enjoyed, do we need to make a
fundamental change to the way we see the position of the 'middle
classes'?
- 1.2
- These are grand questions, outside the scope of, but motivating,
this paper: by exploiting work-life history data
to examine the longitudinal consequences of class, we can begin to
address these issues. In particular, can we find evidence of
fundamental change in the patterns of longitudinal security of
different class locations? Comparing successive cohorts' careers,
can we find systematic change in the prospective 'life chances'
that class location at a particular time confers?
- 1.3
- This paper reports an analysis of class location and its
consequences, in particular the professional-managerial class or
'salariat', at different points in the life cycle, seeking
evidence of change in the pattern of association across cohort (and
therefore through historical time), using British Household Panel Study retrospective
work-life history data.
 Class as a Contested Concept
Class as a Contested Concept
- 2.1
- As a sociological concept class has a long pedigree, playing an
important role in some traditions, vigorously rejected by
others. This is as true now as ever, with a resurgence of
intellectual and popular debate about the applicability of the
concept to late twentieth century society. Opponents of class
analysis have claimed variously that it carries a lot of Marxist
and historicist baggage, or is otherwise demonstrably irrelevant to
the analysis of contemporary societies (e.g.,
Hindess 1987; Turner 1989;
Pahl 1989, 1993;
Sørenson 1991; Pakulski and Waters 1996). Other factors,
such as gender, race, housing tenure and consumption
(Saunders; 1990), lifestyle or preferences (Hakim; 1998)
are claimed to supersede, rather than supplement it. Proponents of
class analysis either reject these claims outright, or assert that
certain of the targets attacked are peripheral to the core concept
of class (especially Goldthorpe and Marshall 1992; see also
Breen and Rottman 1995;
Scott 1994,
1996; Marshall 1997).
- 2.2
- An important element of the debate has concerned recent changes in
employment conditions of professional-managerial workers, altering
or even destroying some of their characteristic advantages; this
perception is also widespread in journalism and management
literature (e.g., Handy; 1994). To a significant
extent these claims are prompted by perceptions of change in the
way large organisations treat their white collar employees:
practices such as the 'de-layering' and 'downsizing' of the late
1980s and early 1990s are adduced as evidence that the security and
predictability of the traditional bureaucratic career no longer
apply, as organisations are becoming capable of, and the market is
demanding, closer and more exploitative control of higher
white-collar workers. One could say that the inexorable progress of
the 'iron cage of bureaucracy' has come to degrade the position of
the bureaucrats themselves.
- 2.3
- Some of this corporate re-structuring is likely, of course, to have
been driven by the business cycle or other entirely market-based
processes, but there is a clear tension in the employment situation
of members of the salariat. That is, the impossibility of
close control of their day-to-day work gives them an advantage
which their employing organisations have a substantial incentive to
overturn, where it becomes possible. Thus it is reasonable that,
over time, certain occupations will move from a service
relationship to a more constrained one. However, it is far less
plausible that the service relationship as a whole could somehow be
overturned by organisational and technological changes: the service
relationship is a solution to a quite general problem of control
(see Goldthorpe; 2000).
- 2.4
- The growth in size in the salariat is impressive: in the data
reported below we see a rise in salariat membership at age 35 from
less than 15 percent for men in the oldest cohort (born before
1920) to 37 percent for men in the youngest cohort (born in the
1950s). For women the rise is of similar magnitude from a lower
base, 12 to 27 percent. Between the 1950s and the 1990s the
salariat has thus more than doubled in size. Growth of this
magnitude suggests certain consequences. First, the incentive for
employing organisations to redefine the service relationship has
become more significant simply because it is more widespread.
Second - and this may be na´ve sociology - as the group becomes
larger one suspects it must lose some if its Úlite status; at any
rate the suspicion arises that in some respect this growth of
advantage is more apparent than real and that the nature of
service-class occupations is deteriorating in some measure as they
become more common. More formally, it is plausible that the means
of the expansion of the salariat, which is largely the growth of
large-scale organisations, is also the means of enforcing less
advantageous conditions on it. Therefore it becomes important to
look for evidence of historical change in the characteristics of
the salariat, ideally with a source of information that is
consistent over time.
- 2.5
- There is another relevant thread in the literature on class, and in
particular on the salariat: among writers who broadly endorse class
analysis, the concept of the salariat as a homogeneous group has
been criticised, and the argument made that professional and
managerial occupations constitute two separate clusters of class
locations (Halford and Savage; 1995; Mills; 1995; Savage et al.; 1992). It is clear that
the work-life trajectories of professional and managerial workers
are relatively distinct (despite evidence of increasing movement
between these categories), though intergenerationally they are more
homogeneous. Theoretically the argument starts from the idea that
classes can be distinguished according to the different sorts of
assets they possess (drawing in particular on the work of Erik Olin
Wright (1985)), and the specialised, credentialled,
skill assets professionals hold are argued to have different
consequences from the organisational assets of managers
(Butler and Savage; 1995a). While this is not the place to debate the
merits of assets versus employment relations as the underpinning of
class (and differences between professionals and other white-collar
workers are not directly dealt with in the analysis below), the
fact that there are distinguishable subgroups within the salariat
and that their proportions are changing, is an important potential
dynamic of change that has to be taken into account. As will be
seen below, the disproportionate growth of non-professional
salariat occupations (and indeed, of professionals with the
employment status of employees) is one of the likely sources of
change in the 'average' characteristics of the class.
- 2.6
- Thus we see that the applicability of class to late
twentieth-century society is widely contested, with particular
focus on the changing conditions of the salariat. Even among class
analysts, the status of the salariat as a homogeneous category has
been contested. So what has been the experience of the
salariat?
 Class as a Longitudinal Concept
Class as a Longitudinal Concept
- 3.1
- In much existing sociological work, class as a measure is an
attempt to use cross-sectional data to pick up important aspects of
likely longitudinal experience. This is clear even in Weber's
development of the concept of life chances (Weber; 1968):
positions vary in their likely consequences throughout the life
course (the concept is partly probabilistic, but also very clearly
longitudinal). This is also more or less explicit in writers like
Goldthorpe (e.g., Erikson and Goldthorpe; 1992; Goldthorpe; 1987) or Scott (1996), though
of course, for all these writers there is much more substance to
the concept of class than longitudinal predictive power.
- 3.2
- The main tool of quantitative sociology is the cross-sectional
survey, something that has both strengths and weaknesses. Among the
weaknesses of this perspective are the difficulty in causal
reasoning based on a snapshot, the potential transience of the
observed conditions, and the fact that time and the processes of
the lifecourse tend to be obscured. The use of social class in
empirical research (be it the Registrar-General's Social Class or a
theoretically based scheme such as Goldthorpe's or the new ONS
Socio-Economic Classification (the NS-SEC,
see Rose and O'Reilly; 1998)) is often oriented to getting around the second of these,
transience, by identifying current characteristics associated with
longer-term outcomes - for instance, class can be a better
predictor of life-time income than current income is.
- 3.3
- Longitudinal data, on the other hand, allow us to avoid some of
these problems. Data about conditions at more than one time point
allow us the luxury of committing the 'post hoc ergo propter hoc'
error: if B follows A in time, to claim that A causes B.
Cross-sectional data that show association between A and B do not
allow us to choose between 'A causes B' and 'B causes A' but with
longitudinal data if we can show that B happens before A, we can at
least exclude the claim that A causes B. Also with longitudinal
data, transience (or durability) becomes something we observe,
rather than a weakness in the data. For instance, we can see how
people move in and out of poverty over time rather than report a
simple poverty rate (Jenkins and Jarvis; 1998). A further important
advantage of longitudinal data from a sociological perspective is
the re-inclusion of time, as calendar, cohort and lifecourse. The
re-inclusion of lifecourse is perhaps the most valuable
contribution of longitudinal data. The cross-sectional measurement
of class, for instance, is a pretty thin thing, compared with the
richer picture of the life-long trajectory we can derive from
longitudinal data.
- 3.4
- The recent increase in availability of longitudinal
data1 makes it
necessary to look again at class as a longitudinal concept. In
particular it provides the opportunity to examine the association
of class with longitudinal outcomes, to validate it or replace it
with lower-level concepts where appropriate, and to better
understand the mechanisms by which it bears on longitudinal
experience. That is, having longitudinal information means it is no
longer necessary to use class as a proxy for its longitudinal
consequences, but also that we can examine these very longitudinal
consequences.
- 3.5
- This paper seeks to examine the situation of the
salariat in British society in the mid- to late-twentieth century,
using longitudinal data to look for evidence of change in its
consequences across the decades. If the critics of class analysis
are right (in particular those who argue that class has
become irrelevant) we should see a waning of its association
with later states. It may be too early to test the claims of those
who see very recent change as fundamental (i.e., if the 'job for
life' has recently disappeared, we will have to wait some portion
of a lifetime to see the consequences) but if the changes in
employment conditions are profound it is likely that some evidence
of the process should be visible. But even if we accept the
fundamentals of class analysis, we have to ask to what extent the
extraordinary growth in white-collar occupations has had on the
nature of the salariat, both in absolute terms and in terms of the
changing mix between professional and managerial occupations.
 Class versus 'General Status'
Class versus 'General Status'
- 4.1
- Social mobility research conventionally analyses square tables
relating class position at two time points. However, because of the
present interest in the stability and meaning of the
measure of class it makes sense to displace the conventional method
with an analysis that relates the class measure, in particular the
salariat, with phenomena to which it is understood to be causally
linked. That is, it is interesting to relate the salariat to
states the likelihood of entry to which is part of the
'life-chances' its membership is taken to affect.
- 4.2
- Therefore the main analysis reported is of what may be called
'general status', comprising a set of states including being in a
salariat occupation, being unemployed and so on (see below for
fuller detail). A parallel analysis using conventional class
categories is also carried out, in order to make clear the effect
of using the non-conventional categories. Since conventional class
analyses tend to show little change in the pattern of association
over time, it is important to identify the extent to which change
evident in the new analysis is due to the different categories
used, and how much is due to change in the data which will also
show up in a conventional analysis.
 Data and Method
Data and Method
- 5.1
- The data set used to address this issue is the British Household Panel Study, and in
particular, its work-life history components. The BHPS is
primarily a panel study, and as such collects detailed labour
market status histories during the period of the panel (September
1991 to the present, and continuing), but it also collected two
retrospective labour-market histories: in its second year it
collected a comprehensive employment-status history, covering all
spells since first leaving full-time education, and in its third
year it collected information on all jobs held. By combining the
two (see Halpin; 1998) into a single history, and then
integrating that with panel-derived data, a data set can be
constructed with enough information to look at class position in
the context of labour market status, and to examine, for instance,
the subsequent pattern of unemployment conditioned on class at a
given time. There are many possible ways of conducting such an
analysis, but because of problems of recall bias (see next section)
this paper examines the pattern of association between the status
at two time points, separated by a 10-year span (analysis in terms
of durations or transitions will be more severely affected by
recall bias than that in terms of status at particular moments). If
class is a good predictor of future states, we should find a strong
relationship, even over a ten-year period.
Figure 1:
Cohort, age and historical time
|
 Bias
Bias
- 6.1
- Measurement error is an ever-present problem in survey data, and in
longitudinal and especially retrospective data it is particularly
significant, in the form of recall bias. While there may not be a
simple relationship between length of the recall period and the
amount of error, there is certainly an association. As
Figure 1 shows, the present data set may involve
recall periods up to 70 years, for the very oldest members of the
earliest cohort remembering their state at age 25 (though for most
respondents the period is much less). What is damaging
from the analyst's point of view is that the length of recall is
directly associated with cohort, and thus apparent cross-cohort
change may simply be due to measurement error. However, given the
sorts of biases that can be expected to operate, this problem will
be more acute for certain forms of analysis than others.
Paull (1996) makes a number of hypotheses about how
recall error might bear on retrospective data:
- Recall error may depend on the length of the recall period
- Short spells are more likely to be forgotten
- Spell durations will be exaggerated
- Transitions will be under-reported
- Unemployment will be under-reported.
- 6.2
- Elias (1997) has corroborated the latter point in
detail, for the BHPS and for other retrospective data sets. He
finds the recall of unemployment to be particularly poor, and to
tail off sharply as the recall period extends. Apart from the poor
recollection of unemployment, the other effects suggested will be
particularly damaging for analyses of duration, such as hazard
models, or models that focus on transitions. Thus a model that
shows the hazard of leaving a job to be higher for younger cohorts
cannot be trusted: it is as likely that younger cohorts simply
remember more job changes.
- 6.3
- However, if instead of spells, durations and transitions, we use
the retrospective data to obtain estimates of respondents' states
at given times, we avoid some of the most important problems. There
will still be measurement error, and it will still be associated
with cohort: older cohorts will show less unemployment, and more of
their reports will be wrong in general. But we will not be
depending on the absence of error over the entire spell, as we
would when using hazard models (i.e., if a spell covers an omitted
period in another state, its duration will be much greater than it
should be). Therefore the following approach is used in this paper:
for each respondent the states at age 25 and at age 35 are
extracted and the relationship between them modelled. With a
ten-year separation, the point estimates of state can be assumed to
be reasonably independent. That is, if the age-25 state is
erroneous it is not likely that the age-35 state will be wrongly
reported for the same reason. However, it is not impossible, nor is
it impossible that the state correctly reported for one age is also
reported for the other. Nevertheless, this approach is less
vulnerable to the sorts of data-quality problems anticipated.
 The Method
The Method
- 7.1
- The methodological paradigm this paper uses is one of association
models of state at age 25 and age 35 (and in some cases age 25 and
age 40, lengthening the span at the expense of losing approximately
half of the youngest cohort), specifically, loglinear models of
square turnover tables, with mobility over a
ten-year span. In particular, the focus is on how the association
changes across cohort.
- 7.2
- Because of the interest in class, it would seem logical to model
mobility between class categories, and this is indeed done in
parallel with the main analysis. But there are several reasons why
this is not enough. Primarily, we are interested in issues relating
to change in the nature of class, and to model only in terms of the
categories of interest makes it hard to see how they may be
changing. Secondly, the way respondents are assigned to class
categories tends to obscure information relevant to this analysis.
For instance, conventionally respondents are assigned to the
category appropriate for their current or last occupation
and employment status. This has the consequence that unemployment
and non-employment disappear which, while appropriate in many
contexts, is a drawback for analysis that might consider entry
to these states as interesting outcomes.
- 7.3
- Therefore the primary analysis is in terms of the following set of categories:
- In a salariat occupation (i.e., professional/managerial)
- In a non-salariat occupation
- Unemployed
- Not in the labour force.
In practice these categories are supplemented by
respondents in employment but without occupational information, and
therefore not assignable to a class category.2
It is important to include this category as such recall
discrepancies may be associated with cohort, and its exclusion may
bias the results.
- 7.4
- A secondary advantage in using this more general set of categories
is that the sample is slightly larger, as there are respondents for
whom the class variable is missing at one or other age (due, for
instance, to never having been in the labour force).
- 7.5
- Given that the concern with the changing nature of class focuses to
a large extent on the changing nature of the service class (or
salariat), either due to its enormous historical increase, or due
to changes in the organisational context of white-collar work,
class enters this scheme as a division between the salariat and all
other classes.
Table 1: The general status variable
| Category |
Description |
|---|
| 1 |
In a salariat occupation |
| 2 |
In a non-salariat occupation |
| 3 |
Employed, occupation not known |
| 4 |
Unemployed |
| 5 |
Not in the labour force |
| |
Table 2: The reduced version of the EGP class scheme
| Class |
Description |
|---|
| I-II |
The 'salariat': professional and managerial employees |
| III |
Routine non-manual employees |
| IV |
Self-employed and small employers, and farmers |
| V-VI |
Supervisory and skilled manual employees |
| VII |
Semi- and unskilled manual employees, industrial and agricultural |
Note:
This is based on the seven category EGP version of the
Goldthorpe class schema, described in Erikson and Goldthorpe (1992),
pp. 35ff, especially figure 2.1.
- 7.6
- Tables 1 and 2 summarise the categories of
the two variables. The class categories in Table 2 are
based on the Goldthorpe class schema (see
inter alia Erikson and Goldthorpe; 1992) but rather than use his seven-category
version, we have collapsed the two agricultural classes (farmers
and agricultural labourers) into their non-agricultural analogues
(classes IV and VII, respectively), since agriculture is
numerically unimportant in Britain.
Table 3: Cohort by sex
| Cohort |
General status | |
Class |
|---|
| |
Men |
Women |
Total | |
Men |
Women |
Total |
| 1900-19 |
298 |
507 |
805 | |
231 |
347 |
578 |
| 1920-29 |
486 |
600 |
1086 | |
401 |
499 |
900 |
| 1930-39 |
524 |
597 |
1121 | |
480 |
498 |
978 |
| 1940-49 |
745 |
872 |
1617 | |
694 |
768 |
1462 |
| 1950-59 |
803 |
890 |
1693 | |
761 |
775 |
1536 |
| Total |
2856 |
3466 |
6322 | |
2567 |
2887 |
5454 |
Note: The numbers in each
analysis differ, primarily because of missing class information.
 Descriptives
Descriptives
- 8.1
- Though the BHPS nominally has of the order of 10,000 respondents,
the sample used in this analysis is somewhat smaller. This is
primarily because we restrict ourselves to the 7,000 or so for whom
we have retrospective life-history data. Missing values reduce this
sample further to c.6,300 for the general status analysis
and c.5,450 for the class analysis. These respondents are
distributed across the five cohort groups (those born before 1920,
and thereafter on a decennial basis until 1959) as shown in
Table 3: women's greater longevity is evident in
their over-representation in the earlier cohorts.
Table 4: Status at 25 by status at 35, men and women
| Status at 25 |
Status at 35 |
|
|---|
| |
Salariat |
Non-salariat |
Employed (job not known) |
Unemployed |
Non-employed |
Total |
| Men |
|
|
|
|
|
|
|---|
| Salariat |
507 |
32 |
2 |
9 |
9 |
559 |
| Non-salariat |
129 |
1573 |
10 |
56 |
39 |
1807 |
| Employed (unknown) |
12 |
15 |
179 |
13 |
5 |
224 |
| Unemployed |
2 |
17 |
3 |
16 |
5 |
43 |
| Non-employed |
61 |
109 |
24 |
2 |
27 |
223 |
| Total |
711 |
1746 |
218 |
96 |
85 |
2856 |
| Women |
|
|
|
|
|
|
|---|
| Salariat |
242 |
26 |
2 |
3 |
120 |
393 |
| Non-salariat |
59 |
743 |
6 |
8 |
466 |
1282 |
| Employed (unknown) |
15 |
17 |
76 |
0 |
104 |
212 |
| Unemployed |
4 |
6 |
1 |
14 |
3 |
28 |
| Non-employed |
95 |
545 |
59 |
6 |
846 |
1551 |
| Total |
415 |
1337 |
144 |
31 |
1539 |
3466 |
- 8.2
- Table 4 shows the relationship between general
status at age 25 and age 35, by sex, for the whole sample. Looking
at the marginals (i.e., the row and column totals) it is clear that
for men the most important state is non-salariat employment - at
each age, and indeed the largest single cell in the table is that
indicating presence in this state at both ages. For women the
largest category at each age is non-employment, closely followed by
non-salariat employment, with the corresponding diagonal cells
being the largest. Whereas for men the concentration in one
category means that more than half the sample are
'immobile'3 in non-salariat employment, much more of the
cases in the women's table are off-diagonal, particularly in cells
representing movement between the two largest categories. This is
not to say that there is not a lot more going on: e.g., for both
sexes movement from non-salariat to salariat employment is
relatively common (but the movement is not symmetrical: either
because of life-cycle effect - an upgrading of occupational status
between age 25 and age 35 - or the retentiveness of salariat
occupations, movement from salariat to non-salariat occupations is
less common).
Table 5: Class at 25 by class at 35, men and women
| Class at 25 |
Class at 35 |
|
|---|
| |
I-II |
III |
IV |
V-VI |
VII |
Total |
| Men |
|
|
|
|
|
|
|---|
| I-II |
549 |
11 |
16 |
4 |
6 |
586 |
| III |
63 |
177 |
14 |
9 |
17 |
280 |
| IV |
3 |
3 |
209 |
8 |
8 |
231 |
| V-VI |
68 |
12 |
45 |
591 |
74 |
790 |
| VII |
33 |
13 |
58 |
65 |
511 |
680 |
| Total |
716 |
216 |
342 |
677 |
616 |
2567 |
| Women |
|
|
|
|
|
|
|---|
| I-II |
434 |
30 |
8 |
5 |
10 |
487 |
| III |
99 |
1085 |
41 |
23 |
120 |
1368 |
| IV |
2 |
5 |
48 |
0 |
2 |
57 |
| V-VI |
8 |
23 |
11 |
173 |
43 |
258 |
| VII |
15 |
95 |
15 |
31 |
561 |
717 |
| Total |
558 |
1238 |
123 |
232 |
736 |
2887 |
- 8.3
- Table 5 shows the analogous table for the
five-category class variable (described in Table 2).
For men and women, and at both ages, this is a much more even
distribution, mostly because the 'non-salariat' is spread over four
classes. Nonetheless we see a good deal of immobility, with well
over half the men represented in the I-II, V-VI and VII
diagonal cells, and over 1,000 of the c.2,900 women immobile
in III, routine non-manual work. Again, we can see some evidence
of upward mobility, in the greater incidence of moves into the
salariat than out.
- 8.4
- However, simple inspection is not adequate to perceive structure
that is not simply a reflection of the overall distribution at each
age: for this we need to explicitly model the association.
Moreover, when we add the dimension of cohort to each table
(raising the number of cells in each from 25 to 125) even
inspection becomes difficult, and it is infeasible to detect
changing patterns in the relationship between early and late
states. Nonetheless, inspection of data is always to be
recommended, and to this end Figures 2 and
3 present the tables in a graphical form, designed to
highlight the pattern of association between early and late states
in each cohort in such a way that broad cross-cohort (and
male-female) differences are relatively easy to see. Each
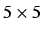 panel of the figures represents a
particular cohort and sex, in the same format as
Table 4. In each panel, the area of the boxes is
proportional to the percentage in each cell, and thus the total
area of the boxes in each panel is the same (empty cells are
indicated by circles). This facilitates comparison across panels,
as the effect of cohort size is eliminated.4
panel of the figures represents a
particular cohort and sex, in the same format as
Table 4. In each panel, the area of the boxes is
proportional to the percentage in each cell, and thus the total
area of the boxes in each panel is the same (empty cells are
indicated by circles). This facilitates comparison across panels,
as the effect of cohort size is eliminated.4
- 8.5
- Looking first at Figure 2, at the column for men, we
can see that the diagonality apparent in Table 4 is
repeated within each cohort. What is interesting is to glance down
the column and see how this pattern changes: the amount of
off-diagonal ink does not change much, with one exception: cohorts
1 and 2 have substantial numbers not in the labour force at age 25
who move into the labour force by age 35. The bulk of these
individuals were in the armed forces: a clear period effect. The
distribution of ink on the diagonal shifts too: in earlier cohorts
category 3 is sizeable, but it declines to very small numbers by
cohort 5. This is the incomplete-data category, where we do not
know the occupation, and it does, as expected, increase with length
of recall period. Otherwise, non-salariat occupations are much
more common than salariat occupations, but this declines sharply
across cohort: by cohort 5 the ratio is closer to 2:1 than the 8:1
seen earlier. Overall these are very highly patterned tables, with
the vast majority of cases residing in two or three diagonal cells
(this causes certain problems with estimation: see
appendix D below).
- 8.6
- When we look at the column for women, we see far less diagonality
in all five cohorts. Women move in and out of the labour force
for a variety of reasons, so the row and column indicating
non-employment are as well-populated as the diagonal. Tracking down
along the cohorts we can see a certain but not dramatic growth in
salariat employment, and a decline in the indeterminate employment
category. The most dramatic change is probably the decline in
immobility in non-employment: there is far more movement into
employment from this category in later cohorts.
- 8.7
- Turning our attention to Figure 3 we can see how
different the class tables are. The first thing to note is how now
both sexes exhibit substantial diagonality. In the case of women,
this is because of excluding the effect of non-employment. For all
the diagonality, however, the incidence of zero cells is less than
in Figure 2. Looking at men, the cross-cohort change
is a move from a predominance of manual work (classes V-VI and
VII) to one of salariat employment. For women, there is a
steady decline in unskilled work, class VII, which probably
reflects the decline in domestic service. In all cohorts, females
outside this class are largely in routine-non manual work
(class III), and to a lesser extent in the salariat. Another
visible feature is the apparent increase in outflow from routine
non-manual, in particular to the salariat.
- 8.8
- However, while this exercise provides an overview of the structure
of the data, it is next to impossible to see change in the
relationship between status at 25 and at 35 that is not driven by
the substantial changes in distributions of these states. This
requires formal modelling of the tables.
 Models
Models
- 9.1
- The same set of models is fitted to both data sets, in an attempt
to test for cross-cohort change in the pattern of association. The
models are chosen so that the contrasts between them will pick up
different possible forms of change. All models are fitted
separately for men and women. Results are presented below for
general status, and class, for the age spans 25-35 and 25-40 (see
Tables 6 and 7, discussed
below).
- 9.2
- More formal descriptions of the models and their relations are
available in an appendix (in appendix A;
hyperlinks to this appendix are present in all references to the
models in the main text).
- 9.3
- Eight distinct models are considered. (For a more formal
presentation of the models see appendix B.)
Model 1 is that consisting of all two-way
interactions (and, implicitly, their first-order components). This
can be considered a base model against which more interesting
models can be compared. It takes account of the fact that early
status is associated with late status, and both are associated with
cohort (that is, it controls for the fact that, for instance, the
distribution of status at age 25 is different across the different
cohorts). However, it does not allow the relationship between early
and late status to change across cohort: insofar as the model fits
well it asserts that though the distribution of states (at both
ages) may change substantially, the underlying association between
them - the pattern of odds ratios in each cohort-specific subtable
- stays the same. In social mobility terms (Erikson and Goldthorpe; 1992, pp. 55ff)
the pattern of relative mobility rates is constant.
- 9.4
- Having fitted all the two-way interactions, the next logical step
appears to be to fit the three-way interaction between status at
25, at 35 and cohort. However, this yields the saturated model,
which fits the data exactly, with no degrees of freedom and no
explanatory power. Instead the next seven models considered fit
constrained versions, or subsets, of the full three way interaction
in order to test for different aspects of change in the pattern of
association across cohorts. The remaining models are in pairs,
both allowing cross-cohort change in a subset of the
status-at-25/status-at-35 subtable, but one constrained so that the
difference between each successive cohort is proportionately
constant (and thus linear in the logs), the other allowing
unconstrained change. The former, 'trend', model is more
parsimonious.
- 9.5
- The first pair of models focuses on the salariat, by including a
special term for the cells indicating retention therein,
and allowing this to change across cohort. We thus allow the
predicted numbers of cases in the salariat to change across cohort,
over and above the change we would expect from the 2-way
model, model 1. The 'trend' variant is
model 2, which allows this extra change to be
proportional, and the 'free' variant is
model 3, which allows non-monotonic change.
- 9.6
- An equally simple form the change could take is that of an overall
change in immobility: not just the salariat, but all states might
be changing in the same way and to the same degree in their
propensity to hold people at both ages. Models 4
and 5 allow this sort of change, respectively
in trend and non-monotonic form. These can be referred to as
'diagonal' models as they allow change in the number of cases in
the diagonal cells.
- 9.7
- One step less restrictive than these models are
models 6 and 7. These
allow cross-cohort change in immobility, but allow it to be
different for each state. Thus we could find that, for instance,
the salariat is becoming less likely to hold people at both ages
while unemployment becomes more likely to. These models are
generalisations of both the 'salariat' models, 2
and 3, (they allow the salariat and
other diagonal cells to vary) and of the 'diagonal' models,
4 and 5.
- 9.8
- Finally we come to the full trend model, model 8.
Here we allow the full status-at-25/at-35 pattern of association to
vary across cohort, in a trending or log-linear manner. That is,
each cell in the status-at-25/at-35 subtable is allowed to vary in
this trending manner. This allows certain forms of mobility (e.g.,
from the salariat to non-employment) to become more or less common
across cohort, as well as permitting change in immobility as
models 4 to 7 do. The
'free' equivalent of this model is the saturated model,
model 9, which simply reproduces the data with no
explanatory power. 'Trend' models of this form are described in
Payne et al. (1994).
- 9.9
- To recapitulate, we fit a baseline model of no change, and then
four sorts of cross-cohort change in association:
- 1.
- change in salariat immobility
- 2.
- overall change in immobility ('diagonal' models)
- 3.
- state-specific change in immobility and
- 4.
- trending change in immobility and mobility.
- 9.10
- For further detail on the models see the appendix, which contains
- a graph mapping the relationships between the models (section A)
- a slightly more formal presentation of the models (section B)
- a discussion on how to choose between them statistically (section C), and
- a discussion of the problem of sparsity, that is, the
relatively large number of empty cells (section D).
 Results: General status to age 35
Results: General status to age 35
- 10.1
- Table 6 presents results for the models of
general status.
For each model, the significance of its improvement in fit is
given, relative to the immediately simpler model (this is for
model 2 over model 1,
model 3 over model 2,
model 4 over model 1,
model 5 over model 4,
model 6 over model 4,
model 7 over model 6, and
model 8 over model 6; see
appendices A and B to clarify the
logic of this set of comparisons).
Table 6: Fitting the general status tables
| |
|
Significance
of improvement in fit over next simpler model |
|
| |
|
25-35 | |
25-40 |
| New |
Simpler |
|
| |
|
|
| Model |
Model |
Men |
Women | |
Men |
Women |
|---|
| 2: Salariat (trend) |
1 |
0.001 |
0.000 | |
0.002 |
0.002 |
| 3: Salariat (non-monotonic) |
2 |
0.339 |
0.059 | |
0.059 |
0.059 |
| 4: General immobility (t) |
1 |
0.827 |
0.000 | |
0.004 |
0.000 |
| 5: General immobility (n-m) |
4 |
0.000 |
0.065 | |
0.000 |
0.511 |
| 6: State-specific immob. (t) |
4 |
0.000 |
0.020 | |
0.000 |
0.002 |
| 7: State-specific immob. (n-m) |
6 |
0.002 |
0.074 | |
0.019 |
0.027 |
| 8: Full trend |
6 |
0.000 |
0.048 | |
0.002 |
0.300 |
Note: The models are
described in the text. The p-values are the significance of the
improvement in fit over the next simpler model. Counts are
adjusted so that zero values are incremented by 0.01. Results
with raw counts are given in Table A.1.
- 10.2
- Looking first at the figures for men, we see that
model 2 improves the fit significantly: allowing
salariat immobility to vary in a trending fashion fits better than
the 2-way model (of no cross-cohort change). A trending effect is
sufficient: non-monotonic model 3 fits no better than
model 2. A single trending effect for the main
diagonal (model 4) is not supported, but a 'free'
effect is (model 5). Allowing separate
trending effects for each diagonal cell (model 6)
fits much better than the single trend;
model 7, where the change is allowed to be
non-linear, fits better again. Model 8, the overall
trend model, also improves on model 6, showing
that the off-diagonal part of the status-at-25/at-35 association is
changing too. Were model 7 nested within
model 8 the trend model would be preferred.
- 10.3
- Thus for men to age 35 we see substantial evidence of change,
including a trending change in salariat immobility, differential
and non-linear change in immobility outside the salariat, and
change also in the off-diagonal association.
- 10.4
- When we look at the results for women we see a broadly similar
picture.
The main difference is that model 4 improves over
model 1, even more than model 2
does: change in immobility in general is not largely
accounted for by change in salariat immobility, though there is
some evidence of a trending salariat effect. The 'free' single
diagonal effect of model 5 is only marginally
better than the trend, but the multiple diagonal trend
(model 6) fits better, and again the 'free'
variant (model 7) is weak. The full trend
model is a very marginal improvement over
model 6. Thus for women the picture is dominated
by a trending change in general immobility.
Table 7: Fitting the class tables
| |
|
Significance
of improvement in fit over next simpler model |
|
| |
|
25-35 | |
25-40 |
| New |
Simpler |
|
| |
|
|
| Model |
Model |
Men |
Women | |
Men |
Women |
|---|
| 2: Salariat (trend) |
1 |
0.305 |
0.000 | |
0.126 |
0.000 |
| 3: Salariat (non-monotonic) |
2 |
0.059 |
0.797 | |
0.081 |
0.296 |
| 4: General immobility (t) |
1 |
0.006 |
0.000 | |
0.006 |
0.000 |
| 5: General immobility (n-m) |
4 |
0.069 |
0.420 | |
0.006 |
0.042 |
| 6: State-specific immob. (t) |
4 |
0.063 |
0.201 | |
0.039 |
0.307 |
| 7: State-specific immob. (n-m) |
6 |
0.334 |
0.084 | |
0.312 |
0.052 |
| 8: Full trend |
6 |
0.858 |
0.416 | |
0.493 |
0.115 |
Note: The models are
described in the text. The p-values are the significance of the
improvement in fit over the next simpler model. Counts are
adjusted so that zero values are incremented by 0.01. Results
with raw counts are given in Table A.2.
 Class to age 35
Class to age 35
- 11.1
- Table 7 presents the results for the same
analysis for the five-category class scheme described in
Table 2. For men the first model to improve on the base
model is model 4, the single diagonal trend. A
free single diagonal effect is hardly any better fitting. Neither
of the multiple diagonal models (6 and
7) improve over models 4
and 5. The trend model fits quite poorly.
Thus we are drawn to a model which identifies cross-cohort change
with a single trending immobility parameter.
- 11.2
- For women we see that allowing salariat immobility
(2) to vary improves fit, but allowing immobility
in general to vary (4) fits much better. Neither
of the 'free' variants of these models improves. Allowing
independent variation in immobility fits no better in trend form
(6) or in free form (7),
and the full trend model (8) is not much better. If
we compare its fit with other models than model 6
(these comparisons are not shown) it improves over the base
model and model 2 but not over
model 4, which can be considered the preferred
model here.
- 11.3
- Thus for women we come down to the same model as for men, but with
the additional knowledge that there is something happening in
salariat immobility.
 Mobility to age 40
Mobility to age 40
- 12.1
- Cutting off career information at age 35 can be justified on
several grounds, but it restricts mobility to a relatively short
span, ten years. It is interesting to
extend the span by 50 per cent, at the cost of losing about half
the youngest cohort. For a start, we can expect somewhat less
diagonality, in that we have given the respondents more time to
change category. Inspection of the data (Figures A.2
and A.3 and Tables A.4 and
A.6, in the appendix) show relatively little
difference from the age-35 data, but there is a little less
diagonality and there are some subtle differences. Modelling these
tables confirms the difference.
- 12.2
- The right-hand panel of Table 6 presents
modelling results for general status to age 40. For men, fit is
improved at nearly every step of the sequence. That is,
model 3 now improves somewhat over
model 2, as does model 5
over model 4: there is evidence of non-linearity
in immobility, both in the salariat and as a general effect. The
less parsimonious models are still favoured, making it a choice
between the non-monotonic state-specific immobility model
(7) and the full-trend model (8).
- 12.3
- For women, the general pattern of significance is repeated, with
the exception that the free single diagonal model
(5) loses all power, as does the trend model
(8).
- 12.4
- Looking at the models of the class tables (in the right-hand of
Table 7), we find less difference than for
the general-status tables. For men, the general pattern of
significance is repeated. For women, apart from a strengthening of
model 5 the picture is largely as for 25-35.
 Reviewing the results: the direction and magnitude of
change
Reviewing the results: the direction and magnitude of
change
- 13.1
- For both men and women, for class and general status, the analysis
shows that there is change in the pattern of association between
early and late state: that is, the patterns of work-life mobility
show evidence of change across cohort that is not driven by the
changing distribution of states. The questions are to what extent
this change relates to the salariat (rather than to, say, mobility
in general) and what form the change takes.
- 13.2
- Reversing the usual order, consider class first: here for both men
and women the model suggesting a simple one-parameter diagonal
trend effect performs well (for men there is some evidence
(p=0.06) that the diagonal effect differs by class). There is no
evidence, that is, that the change can be adequately described by
allowing change in salariat immobility alone, nor that there may be
non-linear change, and only weak evidence (for men) that changes in
immobility vary by state. Nor is there need to allow trending
change in the whole table. Looking at the male parameter estimates
for the diagonal trend effect we see a diagonal effect of
4.01
-0.13k, where k indexes cohort. That is, diagonal cell counts
are raised by a factor of about 48 in cohort 1, falling to about 29
in cohort 5. For women the estimate is
4.92 -0.33k, leading to a
factor of about 98 in cohort 1 and 26 in cohort 5. These are very
dramatic numbers, both in absolute level and in the cross-cohort
decline, but inspection of the data as in Figure 3
will confirm that the tables are very strongly characterised by
diagonality. It is less easy to see how this may be changing across
cohort, which is the justification for the modelling.
Table 8: Trend residuals, men, 25-35, General Status
| |
State at 35 |
|
| State at 25 |
1 |
2 |
3 |
4 |
5 |
|
| 1: Salariat |
0.96 |
1.47 |
2.02 |
1.47 |
1.26 |
|
| 2: Non-salariat |
1.14 |
0.99 |
5.53 |
1.01 |
0.57 |
|
| 3: Employed (unknown) |
0.98 |
2.44 |
0.80 |
0.84 |
0.47 |
|
| 4: Unemployed |
1.41 |
1.05 |
0.66 |
0.84 |
1.39 |
|
| 5: Non-employed |
0.99 |
0.18 |
0.15 |
1.45 |
2.52 |
|
Note: The figures are the ratio
between the fitted value under the trend model and that under the
2-way model, for cohort 5. A figure below 1.0 indicates a
declining trend, and vice versa. Cells with fifteen or
fewer cases in the table as a whole are italicised.
- 13.3
- Turning to the general status tables, we find that the analysis
leads us to a more complex model. For men, we favour the full trend
model, which allows each cell in the status-at-25/at-35 subtable to
trend across the five cohorts. There are rather too many parameters
to present in this model, so instead we look at fitted values, and
in particular how the fitted values for cohort 5 differ under the
trend model from those under the 2-way model.
Table 8 presents the ratio between the trend fitted
value and the 2-way fitted value, for cohort 5. A figure below 1.0
indicates that the trend model predicts a lower value, and
therefore a downward trend across cohort. Looking at the diagonal
we first notice that salariat immobility is indeed reducing, but
that immobility in non-salariat occupations is fairly close to flat
(though reference to Figure 2 will show that this is
a very large cell, and therefore that a small change may refer to
relatively many individuals). Retention in the indeterminate
employment and the unemployment states also falls, more
dramatically than for the salariat. Given that these two states are
affected by recall problems, it is hard to say exactly what is
going on. The biggest figure in the diagonal is 2.52 for
non-employment, which may be entirely driven by the high incidence
of this state in cohorts 1 and 2 (due to war-time military
service). Exits from the salariat seem to go disproportionately to
the indeterminate employment state, but this combination has very
small numbers (as does the salariat to unemployment combination) in
the table as a whole. Slightly more weight can be given to the
increases registered in transitions to non-salariat occupations.
Exits from non-salariat occupations show a more interesting
pattern: while the biggest ratio refers to the relatively rare
category of indeterminate employment, we also see a notable
increase in entry to the salariat, and a drop in entry to
non-employment. Another interesting element is the growth in moves
from indeterminate employment to non-salariat work (but this may
say more about the nature of the recall process than real change).
- 13.4
- The most significant elements of the table, however, relate to
categories 1 and 2: along with the direct consequences of growth in
salariat employment, we see falling immobility, and
disproportionately higher moves in both directions between these
two types of occupation.
- 13.5
- For women, the analysis is simpler, as the preferred model is a
trending change in general immobility: this single effect for all
diagonal cells varies from 6.05 in cohort 1 to 3.28 in cohort 5.
The average level is much less dramatic than in the class tables,
largely because women have always tended to move in and out of the
labour market, but the decline is still big: women are moving in
and out at a greater rate, even after controlling for the greater
numbers of women in the labour market.
 Discussion
Discussion
- 14.1
- This analysis has been motivated by an interest in change in the
longitudinal consequences of class, that is, its effect on
life-chances, especially that of the salariat. The particular
analyses carried out utilise a valuable retrospective data resource
in a narrow but powerful way, and the results suggest that there is
change in the way status at age 25 is associated with status at age
35, across cohorts throughout the mid/late twentieth century. But
what does this finding mean, that association patterns are
changing? What might be happening in the data, and what about the
'grand question' of what is happening to class?
- 14.2
- The finding of changed association, and in particular the increased
mobility out of the salariat, can be interpreted in a number of
ways:
- 1.
- Recall bias;
- 2.
- Changed occupational life-cycle patterns;
- 3.
- Changed composition of the salariat;
- 4.
- Fundamental change to the nature of the salariat.
- 14.3
- Recall bias, though ever-present, is more severe in long-term
retrospective data. Moreover, it is possible to think of mechanisms
by which recall bias would produce patterns like those observed. If
older people are more likely to erroneously report the same
status at both ages, then we may see a pattern of decreasing
immobility in younger cohorts. It is impossible to discount this
mechanism entirely, but certain features suggest that it is not the
whole story. First, the mechanism should lead to increased mobility
in general (such as is seen in the class analysis) but cannot be
expected, a priori, to 'explain' the increased salariat
mobility in the general-status analysis, nor the overall pattern of
trending change for men (similarly the strong increase in women
cycling in and out of the labour force has nothing to do with
recall). Secondly, extending the age-span to 25-40 results in a
rather more complex pattern of change, suggesting that the analysis
is sensitive to the increased time the life-course mobility
processes operate (if the change was entirely driven by recall bias
it should not differ much from the 25-35 analysis). Thirdly,
experimenting with dropping the oldest cohort from the analysis
does not significantly alter the results: to the extent that recall
bias is a problem this cohort will be by far the worst affected.
Fourthly, this analysis is designed to minimise the effect of
recall bias, by comparing paired time-points rather than durations
or patterns of transitions, each of which will be much more
severely affected. In sum, while recall bias can never be
discounted it cannot be taken as driving the results.
- 14.4
- The remaining three interpretations, in contrast, stand as
sociologically meaningful observations about changing class
processes, though in increasing order of theoretical interest.
First, the patterns we see may be driven by the changing
occupational life-cycle. That is, though nominally like is compared
with like by analysing the same age span, the rise in average
school-leaving age may mean that the significance of status at age
25 is not static. In older cohorts, 25 year-olds will have had a
longer time to get established in work, whereas younger cohorts
will be more likely to be still settling in. To the extent this is
true, a pattern of decreasing immobility should be apparent,
perhaps especially for the salariat, whose members will in general
have more education.
- 14.5
- This in itself would be a sociologically interesting change, and one
with substantive consequences for the operation and experience of
class through the lifecourse. If we spend longer preparing to enter
the labour force, and therefore experience the instability of the
early years of labour force participation at later ages, then
clearly the effect of class in at least part of the lifecourse has
changed. Moreover, it is possible that the growing postponement of
entry with the consequent later experience of instability could
weaken the overall effect of class throughout the lifecourse.
However, it is theoretically equally plausible that the other side
of this coin - the fact that the postponement is the result of
spending longer in education - will enhance the longitudinal
consequences of one's class position once in the labour force (for
instance, it may be that the more credentials become the sine
qua non of entry to favoured positions, the more secure the
tenure of credentialled individuals becomes).
- 14.6
- This interpretation suggests further research
utilising this retrospective data set, looking directly at
longitudinal patterns of the early career, or repeating an analysis
such as the present but shifting the age-span according to changing
school-leaving patterns.
But insofar as this was the main or only process underlying change
in the apparent patterns of long-term mobility into the salariat,
there would be, clearly, no substantial implication for class
analysis as an intellectual activity: though an interesting change,
it calls for an adjustment of parameters, not paradigms.
- 14.7
- The second sociologically meaningful interpretation is that the
change in salariat mobility may be driven by its changing
composition. The increase in managerial occupations is greater than
that in professional occupations, so the growth in the salariat has
been accompanied by a change in its composition. It is well known
that managerial and professional occupations differ in their
characteristics, in particular in terms of work-life mobility
(e.g., Mills; 1995; Savage et al.; 1992), with those in managerial occupations
more likely to experience mobility to other categories.
This difference has given rise to claims that the salariat should
be sub-divided along this line in Goldthorpe's class scheme, a
claim which has some pragmatic appeal but violates the conceptual
basis of that scheme (Mills; 1995). Butler and Savage
(1995a), however, propose an alternative way of
building up a class scheme, based on different sorts of assets,
such that professionals hold skill assets and managers
organisational assets. There is nothing in the present exercise
that provides any purchase on the question of the relative merits
of assets and employment relations as conceptual bases for a class
scheme, but it is necessary to come to grips with the problem at a
practical level if
- 1.
- sub-groups within the salariat have significantly different
characteristics, and
- 2.
- the relative share of these subgroups changes over time.
- 14.8
- Insofar as these conditions seem to apply (and condition 1 seems to
apply in the context of work-life mobility, in that to a large,
though lessening extent, professional and managerial careers tend
to be distinct, though intergenerational mobility between these
categories is high), there is a case for introducing this
distinction into the analysis. This raises interesting issues about
phenomena such as the growing tendency for persons with traditional
liberal professional occupations (e.g., lawyers) to be employees
rather than self-employed (i.e., partners).
- 14.9
- But there is more to compositional change than the changing
relative shares of these two categories: we also have to be open to
the question of the rise of entirely new occupations in areas such
as information technology (broadly conceived). Are such occupations
likely to have such radically different employment relations (or to
carry such distinctly different skill assets) as not to fit
existing class schemes at all? Or will they match well with
existing occupations? More technologically-determinist views would
tend towards the former option but the truth is likely to be
somewhere in between the two poles.
- 14.10
- To the extent that this issue raises a challenge to conventional
class analysis, and particularly the Goldthorpe scheme, it arises
not from the empirical exercise but in the theoretical domain. That
is, the raw findings test no formal hypothesis to differentiate
between, for example, the Goldthorpe and the Butler and Savage
approaches, but they do stimulate speculation about the processes.
When we speculate about changes arising from changing composition,
be this a changing professional-managerial ratio, or the growth of
novel categories within the salariat, we have to take seriously the
possibility that the salariat may better be thought of as a
grouping of sub-categories with different characteristics and
theoretically distinct bases. However, such speculation does not
require abandoning a unitary defining principle for the salariat
(i.e., the service relationship): a priori the changes may be
as likely homogenising (professionals becoming employees) as
polarising.
- 14.11
- Though the debate, by its nature, resides at a conceptual level,
empirical analyses arising from the present one are likely to throw
light on the theory: in particular, more analysis focusing on the
longitudinal and intergenerational characteristics of subgroups
within the salariat, is called for. It is important that, in doing
so, special attention is paid to the characteristics of 'new'
salariat occupations, as well as to the professional-managerial
divide. It is also necessary that this empirical research works
both at the level of society-wide sample surveys, ideally
longitudinal in nature, and more narrowly focused in-depth
studies of particular milieux, particularly where we have reason to
expect novel circumstances.
- 14.12
- The third of these interpretations represents the strongest
assertion: that the essential nature of the salariat is changing,
that its effect on life chances is not the same across cohort. This
is the strongest claim because it bears on the characteristics of
salariat positions themselves, and what they confer on the
occupant's lifecourse, rather than the relative proportions of
subgroups we already know about, or the relevance of the timing of
observations. Matters of timing can be accommodated quite easily,
insofar as the consequences are limited to particular parts of the
lifecourse. Matters of changing composition, insofar as it affects
the average outcome, indicate a need to take account of the
subgroups where this is empirically warranted. To the extent that
changing composition is brought about by the emergence of new
categories with new characteristics, there is a need for new
research oriented to locating these new occupations, though it is
unlikely that the employment relations attaching to these
categories could be so novel as to overturn existing
conceptualisations of class.
- 14.13
- Thus the most consequential interpretation, and perhaps the hardest
to demonstrate, is that the nature of the individual class
locations that make up the salariat is changing. The present
analysis raises this possibility by showing that there is change in
the association between status at ages 25 and 35, but cannot in
itself separate the competing explanations of changing life-cycle
or compositional effects. To do that is outside the scope of the
paper (which is intended as a starting point for further research),
but what the paper does determine is that there is evidence of
change in the longitudinal effect of certain class categories, to
be observed in retrospective BHPS work-life history data.
- 14.14
- This interpretation, were it to be supported by further empirical
analyses designed to test it, might pose the greatest challenge, if
not to class analysis as such, at least to those forms of it which
claim that the consequences of class positions are effectively
unchanging. Now, while Erikson and Goldthorpe (1992) go
to great lengths to set up and explore the 'common social fluidity
model', which suggests that the underlying patterns of social
mobility are largely constant across time and (developed)
societies, they treat it as an important empirical
regularity and not as a theoretical requirement. Moreover, they
find some systematic departures from the 'common' pattern, usually
attributable to country-specific historical conditions. Certainly,
departures from the pattern are not theoretically ruled out, and
especially not when using more extensive data, as, for instance,
Vallet (1999) has recently done for France with repeated
cross-sectional data. More extensive data, such as Vallet's long
series of contemporaneously collected mobility tables, or long
retrospective individual histories as in the present case, have a
lot more power to elucidate both change over time, and the
processes underlying the structure. Erikson and Goldthorpe
explicitly recognise that an 'empirical regularity' can only be a
starting point for more investigation. This exercise begins one
such investigation, exploiting a particularly rich form of data,
life histories, and raises a number of other questions that can be
directly addressed by further research in a longitudinal
perspective.
- 14.15
- Is class changing? In the narrow terms of this analysis, it may be.
Certainly aspects of the class life-course over the 25-35 age-span
show evidence of change, due to changing life-course patterns,
changing salariat composition, or more fundamental change in the
characteristics of class locations.
Starting from this observation, we need to continue the debate at
the conceptual level, dealing with issues such as the assets
versus employment-relations argument, or other arguments about
changes in the nature of the organisation of occupations such that
the employment relations of the salariat are changing in their
character. Whatever way the theoretical debate goes, it is
necessary that it is couched in terms that allow empirical tests of
its claims and counter-claims. It is also necessary that, in
designing empirical tests of the theory, researchers take account
of time: insofar as class has consequences, they operate temporally
and we now have data and techniques that allow us to deal with
the longitudinal.
One of the main advantages of the present analysis is the
data used to address the issue: work-life histories for respondents
whose experience covers a wide historical time-span. If we are to
address questions of change in the nature of class we need doubly
longitudinal data: longitudinal from the respondent's point of view
in order to observe long-term outcomes, and longitudinal in a
calendar sense, in order to observe the processes in different
periods. In practice such data can only be had by retrospective
means5 and it is
incumbent on those interested in historical change in social
processes to exploit such data to the full.

 Notes
Notes
-
1 There are several different types of longitudinal
dataset, including panel studies which interview the same
random sample of people at regular intervals, cohort
studies which interview a sample of people born in a particular
period, retrospective studies where respondent's recall
their life histories, and linked administrative records
where different official databases are linked to create
longitudinal records. Among panel studies are the US Panel Study
on Income
(PSID),
an influential early example, the British Household Panel Study
(BHPS),
the German Socio-economic Panel
(GSOEP),
the Panel Study of Belgian Households
(PSBH),
and the European Community Household Panel (ECHP), coordinated by
Eurostat.
There are two well-known UK cohort studies, the National Child
Development Study of persons born in 1958
(NCDS)
and the British Cohort Study of persons born in 1970
(BCS70).
Retrospective studies include the UK Family and Working Lives
Survey from 1994
(FWLS)
and the influential German Life History Studies
(GLHS).
Linked administrative studies are less common, but several
Scandinavian countries link tax and social welfare records for
research, and in the UK the Census Longitudinal Study
(ONS-LS)
links information from three censuses with vital registration
records to create anonymised longitudinal data for about
1 percent of the population over a 20-year period.
2
These cases
arise because the data used are drawn from a combined data set
(ljemp) based on the two long-term retrospective work-life
histories in the BHPS, BLIFEMST, which records employment
status and CLIFEJOB, which records occupational
information. In certain cases, these records do not match, and we
end up with employment status information but not occupational,
or vice versa. See Halpin (1998) for details.
3
We will speak of the diagonal in these tables
as indicating immobility. This is inexact: someone who is
genuinely immobile will be represented on the diagonal, but
someone who moves out of his/her status and then back will also
be on the diagonal.
4
For those who
prefer arithmetic to geometry, the raw figures are presented in
Tables A.3 and A.5 in the appendix.
5
Very long panels will give better data (with less
recall bias) over a shorter historical period.

 References
References
-
BISHOP, Y. M. M., FIENBERG, S. E. and HOLLAND,
P. W. (1975).
Discrete Multivariate Analysis: Theory and Practice.
Cambridge, Massachusetts: MIT Press.
BREEN, R. and ROTTMAN, D. B. (1995).
Class Stratification: A Comparative Perspective.
Hemel Hempstead: Harvester Wheatsheaf.
BUTLER, T. and SAVAGE, M. (1995a).
'Assets and the Middle Classes in Contemporary Britain', in
Social Change and the Middle Classses (Butler and Savage; 1995b).
BUTLER, T. and SAVAGE, M. (eds.)
(1995b).
Social Change and the Middle Classses.
London: UCL Press.
ELIAS, P. (1997).
'Who Forgot They Were Unemployed?', Working Paper 97-19, ESRC
Research Centre on Micro-social Change, University of Essex.
ERIKSON, R. and GOLDTHORPE, J. H. (1992).
The Constant Flux: A Study of Class Mobility in Industrial
Societies.
Oxford: Clarendon Press.
GOLDTHORPE, J. H. (1987).
Social Mobility and Class Structure in Modern Britain, 2nd
edn.
Oxford: Oxford University Press.
GOLDTHORPE, J. H. (2000).
'Social Class and the Differentiation of Employment Contracts',
Numbers and Narratives: Essays for a Modern Sociology.
Oxford: Clarendon Press.
Goldthorpe, J. and Marshall, G. (1992).
'The Promising Future of Class Analysis: A Response to Recent
Critiques', Sociology, Vol. 26, pp. 381-400.
HAGENAARS, J. A. (1990).
Categorical Longitudinal Data: Log-Linear Panel, Trend and
Cohort Analysis.
Newbury Park: Sage.
HAKIM, C. (1998).
'Developing a Sociology for the Twenty-First Century: Preference
Theory', British Journal of Sociology, Vol. 49, No. 1, pp. 137-43.
HALFORD, S. and SAVAGE, M. (1995).
'The Bureaucratic Career: Demise or Adaptation?', in
Butler and Savage (1995b).
HALPIN, B. (1998).
'Unified BHPS Work-Life Histories: Combining Multiple Sources into
a User-Friendly Format', Bulletin de Méthodologie Sociologique,
No. 60.
HANDY, C. (1994).
The Empty Raincoat: Making Sense of the Future.
London: Hutchinson.
HINDESS, B. (1987).
Politics and Class Analysis.
Oxford: Basil Blackwell.
JENKINS, S. P. and JARVIS, S. (1998).
'Income and poverty dynamics in Britain', in L. Leisering
and R. Walker (eds.), The Dynamics of
Modern Society: Policy, Poverty and Welfare.
Bristol: The Policy Press, pp. 145-160.
LINDSEY, J. K. (1989).
Analysis of Categorical Data using GLIM, number 56 in
Lecture Notes in Statistics.
Berlin: Springer Verlag.
LINDSEY, J. K. (1995).
Modelling Frequency and Count Data.
Oxford: Clarendon Press.
MARSHALL, G. (1997).
Repositioning Class: Social Inequality in Industrial
Societies.
London: Sage.
MILLS, C. (1995).
'Managerial and Professional Work-histories', in
Butler and Savage (1995b).
PAHL, R. E. (1989).
'Is the Emperor Naked?', International Journal of Urban and
Regional Research, Vol. 13, No. 4, pp. 711-720.
PAHL, R. E. (1993).
'Does Class Analysis Without Class Theory Have a Future? A Reply to
Goldthorpe and Marshall', Sociology, Vol. 27, No. 2,
pp. 253-58.
PAKULSKI, J. and WATERS, M. (1996).
The Death of Class.
London: Sage.
PAULL, G. (1996).
'The Biases Introduced By Recall and Panel Attrition on Labour Market
Behaviour in the British Household Panel Survey', Working Paper 827,
Centre for Economic Performance, London School of Economics.
PAYNE, C., PAYNE, J. and HEATH, A. (1994).
'Modelling Trends in Multi-Way Tables', in A. Dale
and R. B. Davies (eds.), Analyzing
Social and Political Change: A Casebook of Methods.
London: Sage.
ROSE, D. and O'REILLY, K. (1998).
The ESRC Review of Government Social Classifications.
London and Swindon: ONS/ESRC.
SAUNDERS, P. (1990).
A Nation of Home Owners.
London: Unwin Hyman.
SAVAGE, M., BARLOW, J., DICKENS, P. and FIELDING,
T. (1992).
Property, Bureaucracy and Culture: Middle-Class Formation in
Contemporary Britain.
London: Routledge.
SCOTT, J. (1994).
'Class Analysis: Back to the Future', Sociology, Vol. 28,
No. 4, pp. 933-942.
SCOTT, J. (1996).
Stratification and Power: Structures of Class, Status and
Command.
Cambridge: Polity Press.
SORENSON, A. B. (1991).
'On the Usefulness of Class Analysis in Research on Social Mobility
and Socioeconomic Inequality', Acta Sociologica.
TURNER, B. S. (1989).
'Has Class Analysis a Future? Max Weber and the Challenge of
Liberalism to Gemeinschaftlich Accounts of Class', in R. J. Holton
and B. S. Turner (eds.), Max Weber on
Economy and Society.
VALLET, L.-A. (1999).
'Quarante Années de Mobilité Sociale en France:
L'évolution de la Fluidité Sociale à la Lumière de
Modèles Récents', Revue Française de Sociologie, Vol. 40,
No. 1, pp. 5-64.
WEBER, M. (1968).
Economy and Society.
New York: Bedminster Press.
Edited by Guenther Roth and Claus Wittich.
WRIGHT, E. O. (1985).
Classes.
London: Verso.

 Appendix
Appendix
How the models relate to one another
Figure A.1: How the models relate to one another
| The models are arrayed in order of their
parsimony, from the 2-way model at one extreme to the
saturated model at the other. The links between models
indicate nesting, with more parsimonious models being nested
within less parsimonious. Vertical links connect trend/free
pairs of models. Nesting is transitive but not all less
parsimonious models are nested within more parsimonious ones:
for instance, model 8 is not nested within model 7, nor 4
within 3.
Trend/free pairs of models allow cross-cohort variation in the same
component of the state-at-25/state-at-35 association, but differ in
that the 'trend' model imposes the constraint that change is linear
(in the logs) while the 'free' model allows the component to vary
independently in each cohort.
|
Model specifications
Model 1: The 2-way interaction model.
This model implies that the cohort specific patterns of association do
not significantly differ from the overall pattern of association.
It thus serves as a baseline model and is nested within all the
other models discussed.
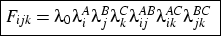
This model takes account of an overall status-at-25/at-35
association, the changing distribution of status at 25 across
cohort and the changing distribution of status at 35 across
cohort.
See model graph A.1
Model 2: The salariat-trend model.
This model implies that there is cross-cohort change in the
patterns of association, which can be summarised as a
trending increase or decrease in immobility in the
salariat.
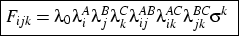
where  is equal to 1 unless status at 25 and
status at 35 are both salariat and is otherwise to be estimated,
with
is equal to 1 unless status at 25 and
status at 35 are both salariat and is otherwise to be estimated,
with  being raised to the power of k, the index of
cohort.
being raised to the power of k, the index of
cohort.
See model graph A.1
Model 3: The salariat-free model.
This model implies allows for cross-cohort change in the
patterns of association, that can be attributed to changing immobility in
the salariat. It differs from model 2 in that the
change can be non-monotonic rather than trending.
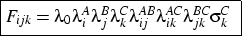
where
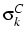 is equal to 1 unless status at 25 and
status at 35 are both salariat and is otherwise to be estimated,
with
is equal to 1 unless status at 25 and
status at 35 are both salariat and is otherwise to be estimated,
with
 having independent values for each cohort.
having independent values for each cohort.
See model graph A.1
Model 4: The diagonal model.
This model implies that cross-cohort change takes the form of a
trending increase (or decrease) in the overall tendency to
immobility: the diagonal cells in general become more (or less)
populated over cohort.
where  is equal to 1 unless i = j, in which case it is
to be estimated.
is equal to 1 unless i = j, in which case it is
to be estimated.
See model graph A.1
Model 5: The diagonal-free model.
This model implies that cross-cohort change takes the form of a
non-monotonic pattern of change in the overall tendency to
immobility: the diagonal cells in general are differently
populated in each cohort. It differs from
model 4 in that the change can be
non-monotonic rather than trending.
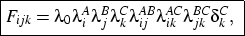
where
 is equal to 1 unless i = j, in which case it is
to be estimated.
is equal to 1 unless i = j, in which case it is
to be estimated.
See model graph A.1
Model 6: The free-diagonal model.
This model extends model 4 by allowing trending
change in immobility that is allowed to be different for each
category. It is also an extension of model 2
which allows immobility for one category only to change.
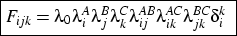
where  is equal to 1 unless i = j, and is otherwise to
be estimated. (
is equal to 1 unless i = j, and is otherwise to
be estimated. (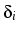 is
equivalent to
is
equivalent to 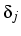 given this condition; the choice of
subscript is arbitrary.)
given this condition; the choice of
subscript is arbitrary.) 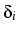 is raised to the power of
k, the index of cohort.
is raised to the power of
k, the index of cohort.
See model graph A.1
Model 7: The free free-diagonal model.
This model is the non-monotonic version of
model 6 and allows immobility to vary across cohort
differently for each category in a non-monotonic manner. It is
thus also an extension of models 5 and
3.
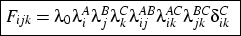
where
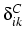 is equal to 1 unless i = j, and is otherwise to
be estimated. (
is equal to 1 unless i = j, and is otherwise to
be estimated. (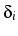 is
equivalent to
is
equivalent to 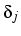 given this condition; the choice of
subscript is arbitrary.)
given this condition; the choice of
subscript is arbitrary.)
See model graph A.1
Model 8: The full-trend model.
This model implies that cross-cohort change in the association is
not restricted to the diagonal, that is, to cells representing
immobility, but that there is also change in the off-diagonal
cells which represent mobility. This change is a trending
change. If we relax this linearity constraint we arrive at
model 9, the saturated model.
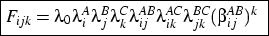
where
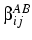 is a term for each element of the status
at 25/at 35 association, raised to the power of k.
is a term for each element of the status
at 25/at 35 association, raised to the power of k.
See model graph A.1
Model 9: The saturated model.
This model implies the association is different in each cohort,
and that this difference is unsystematic. The model exactly
reproduces the data and has no explanatory power. It can be
regarded as the 'free' version of model 8, bearing
the same relation to it as model 5 does to
model 4 or model 3 to 2.
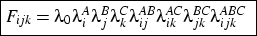
This differs from model 1 in the three-way
interaction term,
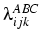 ,
and has no degrees of freedom.
,
and has no degrees of freedom.
See model graph A.1
Evaluating models
Figure A.1 illustrates the relationship between the
models, showing both their relative parsimony - with the
saturated model (not fitted) entirely non-parsimonious, and
model 1 the most parsimonious - and the hierarchical
connections between them (shown by the links). All the models are
'nested' within the saturated model: that is, they are equivalent
to the saturated model with certain of its terms constrained to 1.
Similarly, model 1 is nested within all the other
models, as they are elaborations of it. Nesting is transitive,
that is, if Ma is nested within Mb and Mb within Mc,
then Ma is nested within Mc. Trend/free pairs of models are
shown vertically one above the other.
Nesting is important because it can be shown mathematically that
when one model is nested within another (say, Ma within Mb),
the significance of the improvement in fit in moving from Ma to
Mb is given by the significance of the difference in deviance,
or G2, in conjunction with the difference in degrees of freedom,
asymptotically distributed as  (see, e.g.,
Bishop et al. 1975, pp. 524ff). Where models are not nested, as,
for instance, models 7 and 8,
this relationship does not hold, and insofar as we examine their
difference in fit in these terms it can only be illustrative.
Model 8 is both more general than
model 7, in that it allows change in the
off-diagonal association, and less, in that it restricts the
change in diagonal association to be log-linear (i.e., proportional).
It is, however, slightly more parsimonious.
(see, e.g.,
Bishop et al. 1975, pp. 524ff). Where models are not nested, as,
for instance, models 7 and 8,
this relationship does not hold, and insofar as we examine their
difference in fit in these terms it can only be illustrative.
Model 8 is both more general than
model 7, in that it allows change in the
off-diagonal association, and less, in that it restricts the
change in diagonal association to be log-linear (i.e., proportional).
It is, however, slightly more parsimonious.
Zero cells
As examination of Figures 2 and 3 will
show, there is a relatively high incidence of zero cells in the
tables, more so in the status table than in the class table, and
more so in earlier cohorts than in late. This is partly due to the
very poor long-term recollection of unemployment in the BHPS, a
common feature of retrospective data of this sort. Zero cells
present a problem for loglinear modelling, in particular for models
with many interactions. Part of the problem is that zero cells can
cause numerical instability, with the estimation failing to
converge, and part is that models may report more degrees of
freedom than is strictly correct. That is, where zero cells
contribute no information to the model, they should not contribute
degrees of freedom either. Lindsey (1989) proposes a
method, named DFCT, for correcting the degrees of freedom, by
fitting each model a second time, eliminating those zero cells
whose initial fitted value is very close to zero.
Because it reduces the number of cells in the data, it reduces the
available degrees of freedom. Because this is more likely to occur
in complex models the technique can be regarded as having a
conservative effect (though he revises his interpretation of the
method in Lindsey (1995), its conservative effect holds).
Another technique that is widely
used, primarily to solve convergence problems, is to add a small
constant to all zero cells (for instance, 0.1). While it is easy
and effective, it is not based on statistical theory
(see Hagenaars; 1990, pp. 87ff), and constitutes an alteration,
albeit minor, to the data. An addition of 0.01 is used in the
present exercise.
In the modelling, both of these techniques are applied, and
Tables A.1 to A.2 report results
in quadruplicate, without and with the Lindsey correction, for raw
and altered counts. In general the first are to be preferred
(uncorrected raw counts) but in the analysis adjusted counts are
used throughout, because of estimation problems with the raw
counts.
As can be seen from the tables, to use DFCT would somewhat
increase the likelihood of rejecting the more complex models.
Table A.1:
Fitting the general status tables
| |
Significance of improvement in fit |
| |
| |
|
| |
Age span: 25-35 | |
Age span: 25-40 | |
| |
|
| |
Raw counts |
| Adj. counts |
|
Raw counts |
| Adj. counts |
|
| |
|
| Model |
Plain | |
DFCT | |
Plain | |
DFCT | |
Plain | |
DFCT | |
Plain | |
DFCT |
| Men |
| |
| |
| |
| |
| |
| |
| |
|
| 2: Salariat: |
0.001 | |
0.001 | |
0.001 | |
0.004 | |
0.002 | |
0.002 | |
0.002 | |
0.007 |
| 3: Salariat-f: |
0.345 | |
0.345 | |
0.339 | |
0.190 | |
0.060 | |
0.060 | |
0.059 | |
0.025 |
| 4: Diagonal: |
0.824 | |
0.824 | |
0.827 | |
0.827 | |
0.004 | |
0.004 | |
0.004 | |
0.004 |
| 5: Diagonal-f: |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 |
| 6: Diag-2: |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 |
| 7: Diag-2-f: |
0.002 | |
0.001 | |
0.002 | |
0.001 | |
0.018 | |
0.039 | |
0.019 | |
0.008 |
| 8: Trend: |
-- | |
-- | |
0.000 | |
0.000 | |
0.001 | |
0.048 | |
0.002 | |
0.061 |
| Women |
| |
| |
| |
| |
| |
| |
| |
|
|---|
| 2: Salariat: |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.002 | |
0.002 | |
0.002 | |
0.002 |
| 3: Salariat-f: |
-- | |
-- | |
0.059 | |
0.059 | |
0.059 | |
0.059 | |
0.059 | |
0.059 |
| 4: Diagonal: |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 |
| 5: Diagonal-f: |
0.065 | |
0.065 | |
0.065 | |
0.065 | |
0.511 | |
0.511 | |
0.511 | |
0.511 |
| 6: Diag-2: |
0.019 | |
0.019 | |
0.020 | |
0.020 | |
0.002 | |
0.005 | |
0.002 | |
0.006 |
| 7: Diag-2-f: |
-- | |
-- | |
0.074 | |
0.074 | |
0.026 | |
0.053 | |
0.027 | |
0.019 |
| 8: Trend: |
0.040 | |
0.059 | |
0.048 | |
0.097 | |
0.256 | |
0.403 | |
0.300 | |
0.353 |
| Note: The models are
described in the text. The p-values are the significance of the
improvement in fit over a simpler model, in the following
pattern: 2 : 1; 3 : 2; 4 : 1; 5 : 4; 6 : 4; 7 : 6; 8 : 6. The
symbol '--' indicates a model for which there were estimation
problems arising from zero cells. Adjusted counts have zero
values incremented by 0.01. The DFCT correction weights out zero
cells which have low fitted values, and re-fits the model,
reporting a more conservative fit estimate. |
| |
| |
|
Table A.2: Fitting the class tables
| |
Significance of improvement in fit |
| |
| |
|
| |
Age span: 25-35 | |
Age span: 25-40 | |
| |
|
| |
Raw counts |
| Adj. counts |
|
Raw counts |
| Adj. counts |
|
| |
|
| Model |
Plain | |
DFCT | |
Plain | |
DFCT | |
Plain | |
DFCT | |
Plain | |
DFCT |
| Men |
| |
| |
| |
| |
| |
| |
| |
|
| 2: Salariat: |
0.298 | |
0.298 | |
0.305 | |
0.305 | |
0.123 | |
0.123 | |
0.126 | |
0.126 |
| 3: Salariat-f: |
0.059 | |
0.059 | |
0.059 | |
0.059 | |
0.082 | |
0.082 | |
0.081 | |
0.081 |
| 4: Diagonal: |
0.006 | |
0.006 | |
0.006 | |
0.006 | |
0.006 | |
0.006 | |
0.006 | |
0.006 |
| 5: Diagonal-f: |
0.070 | |
0.070 | |
0.069 | |
0.069 | |
0.006 | |
0.006 | |
0.006 | |
0.006 |
| 6: Diag-2: |
0.058 | |
0.058 | |
0.063 | |
0.063 | |
0.037 | |
0.037 | |
0.039 | |
0.039 |
| 7: Diag-2-f: |
0.322 | |
0.527 | |
0.334 | |
0.334 | |
0.300 | |
0.502 | |
0.312 | |
0.312 |
| 8: Trend: |
0.850 | |
0.850 | |
0.858 | |
0.858 | |
0.474 | |
0.474 | |
0.493 | |
0.493 |
| Women |
| |
| |
| |
| |
| |
| |
| |
|
|---|
| 2: Salariat: |
-- | |
-- | |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 |
| 3: Salariat-f: |
-- | |
-- | |
0.797 | |
0.797 | |
0.295 | |
0.295 | |
0.296 | |
0.296 |
| 4: Diagonal: |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 | |
0.000 |
| 5: Diagonal-f: |
0.416 | |
0.416 | |
0.420 | |
0.420 | |
0.042 | |
0.042 | |
0.042 | |
0.042 |
| 6: Diag-2: |
-- | |
-- | |
0.201 | |
0.201 | |
0.302 | |
0.302 | |
0.307 | |
0.307 |
| 7: Diag-2-f: |
-- | |
-- | |
0.084 | |
0.112 | |
0.052 | |
0.052 | |
0.052 | |
0.052 |
| 8: Trend: |
-- | |
0.395 | |
0.416 | |
0.416 | |
0.088 | |
0.219 | |
0.115 | |
0.246 |
| Note: The models are
described in the text. The p-values are the significance of the
improvement in fit over a simpler model, in the following
pattern: 2 : 1; 3 : 2; 4 : 1; 5 : 4; 6 : 4; 7 : 6; 8 : 6. The
symbol '--' indicates a model for which there were estimation
problems arising from zero cells. Adjusted counts have zero
values incremented by 0.01. The DFCT correction weights out zero
cells which have low fitted values, and re-fits the model,
reporting a more conservative fit estimate. |
| |
| |
|
Figure A.2: Cross-tabulation of cohort by sex by general status, age 25 and age 40.
This is a cross-tabulation with numbers replaced by boxes whose area is proportional to the cell percentage within each 5 x 5 subtable. In each subtable the area of the boxes sums to the same quantity. Empty cells are indicated by circles.
Figure A.3: Cross-tabulation of cohort by sex by class (25-40)
This is a cross-tabulation with numbers replaced by boxes whose area is proportional to the cell percentage within each 5 x 5 subtable. In each subtable the area of the boxes sums to the same quantity. Empty cells are indicated by circles.
Table A.3:
General status, age 25 by age 35, by cohort and sex
| State |
State at 35 |
| | | | | |
| at 25 |
Men |
| Women | | | | | |
| |
1 | 2 | 3 | 4 | 5 | Total | |
1 | 2 | 3 | 4 | 5 | Total |
| Cohort 1 | | | | | | |
| | | | | |
| 1 |
15 | 2 | 0 | 0 | 0 | 17 | |
14 | 2 | 0 | 0 | 18 | 34 |
| 2 |
6 | 128 | 1 | 0 | 15 | 150 | |
3 | 83 | 1 | 1 | 89 | 177 |
| 3 |
1 | 0 | 42 | 0 | 2 | 45 | |
0 | 0 | 23 | 0 | 35 | 58 |
| 4 |
0 | 2 | 1 | 0 | 0 | 3 | |
0 | 0 | 0 | 2 | 2 | 4 |
| 5 |
14 | 53 | 14 | 0 | 2 | 83 | |
1 | 30 | 9 | 0 | 194 | 234 |
| Total |
36 | 185 | 58 | 0 | 19 | 298 | |
18 | 115 | 33 | 3 | 338 | 507 |
| Cohort 2 | | | | | | |
| | | | | |
| 1 |
41 | 2 | 0 | 0 | 0 | 43 | |
24 | 0 | 1 | 0 | 20 | 45 |
| 2 |
14 | 285 | 0 | 1 | 3 | 303 | |
3 | 132 | 0 | 2 | 98 | 235 |
| 3 |
1 | 0 | 58 | 0 | 1 | 60 | |
0 | 2 | 27 | 0 | 14 | 43 |
| 4 |
0 | 1 | 1 | 1 | 0 | 3 | |
0 | 0 | 0 | 4 | 0 | 4 |
| 5 |
20 | 43 | 8 | 0 | 6 | 77 | |
9 | 70 | 14 | 0 | 180 | 273 |
| Total |
76 | 331 | 67 | 2 | 10 | 486 | |
36 | 204 | 42 | 6 | 312 | 600 |
| Cohort 3 | | | | | | |
| | | | | |
| 1 |
91 | 5 | 1 | 0 | 1 | 98 | |
34 | 4 | 1 | 0 | 24 | 63 |
| 2 |
15 | 346 | 1 | 1 | 3 | 366 | |
7 | 109 | 2 | 2 | 82 | 202 |
| 3 |
2 | 1 | 34 | 0 | 0 | 37 | |
4 | 3 | 12 | 0 | 20 | 39 |
| 4 |
0 | 1 | 0 | 0 | 0 | 1 | |
0 | 0 | 0 | 1 | 0 | 1 |
| 5 |
8 | 7 | 2 | 0 | 5 | 22 | |
22 | 103 | 13 | 0 | 154 | 292 |
| Total |
116 | 360 | 38 | 1 | 9 | 524 | |
67 | 219 | 28 | 3 | 280 | 597 |
| Cohort 4 | | | | | | |
| | | | | |
| 1 |
176 | 8 | 1 | 0 | 4 | 189 | |
78 | 5 | 0 | 1 | 24 | 108 |
| 2 |
33 | 434 | 3 | 13 | 4 | 487 | |
14 | 204 | 0 | 3 | 101 | 322 |
| 3 |
2 | 4 | 33 | 6 | 0 | 45 | |
4 | 5 | 6 | 0 | 15 | 30 |
| 4 |
0 | 4 | 1 | 3 | 0 | 8 | |
2 | 2 | 1 | 5 | 0 | 10 |
| 5 |
8 | 1 | 0 | 0 | 7 | 16 | |
27 | 187 | 15 | 2 | 171 | 402 |
| Total |
219 | 451 | 38 | 22 | 15 | 745 | |
125 | 403 | 22 | 11 | 311 | 872 |
| Cohort 5 | | | | | | |
| | | | | |
| 1 |
184 | 15 | 0 | 9 | 4 | 212 | |
92 | 15 | 0 | 2 | 34 | 143 |
| 2 |
61 | 380 | 5 | 41 | 14 | 501 | |
32 | 215 | 3 | 0 | 96 | 346 |
| 3 |
6 | 10 | 12 | 7 | 2 | 37 | |
7 | 7 | 8 | 0 | 20 | 42 |
| 4 |
2 | 9 | 0 | 12 | 5 | 28 | |
2 | 4 | 0 | 2 | 1 | 9 |
| 5 |
11 | 5 | 0 | 2 | 7 | 25 | |
36 | 155 | 8 | 4 | 147 | 350 |
| Total |
264 | 419 | 17 | 71 | 32 | 803 | |
169 | 396 | 19 | 8 | 298 | 890 |
| Grand total |
711 | 1,746 | 218 | 96 | 85 | 2,856 | |
415 | 1,337 | 144 | 31 | 1,539 | 3,466 |
Table A.4:
General status, age 25 by age 40, by cohort and sex
| State |
State at 40 |
| | | | | |
| at 25 |
Men |
| Women | | | | | |
| |
1 | 2 | 3 | 4 | 5 | Total | |
1 | 2 | 3 | 4 | 5 | Total |
| Cohort 1 | | | | | | |
| | | | | |
| 1 |
14 | 2 | 0 | 0 | 1 | 17 | |
17 | 4 | 0 | 0 | 13 | 34 |
| 2 |
8 | 138 | 2 | 0 | 2 | 150 | |
4 | 90 | 2 | 0 | 81 | 177 |
| 3 |
1 | 0 | 42 | 0 | 2 | 45 | |
0 | 2 | 25 | 0 | 31 | 58 |
| 4 |
0 | 2 | 1 | 0 | 0 | 3 | |
0 | 1 | 0 | 1 | 2 | 4 |
| 5 |
14 | 54 | 14 | 0 | 1 | 83 | |
2 | 36 | 17 | 0 | 179 | 234 |
| Total |
37 | 196 | 59 | 0 | 6 | 298 | |
23 | 133 | 44 | 1 | 306 | 507 |
| Cohort 2 | | | | | | |
| | | | | |
| 1 |
39 | 4 | 0 | 0 | 0 | 43 | |
20 | 2 | 1 | 0 | 22 | 45 |
| 2 |
17 | 282 | 1 | 0 | 3 | 303 | |
5 | 145 | 2 | 1 | 82 | 235 |
| 3 |
1 | 1 | 57 | 0 | 1 | 60 | |
0 | 1 | 27 | 0 | 15 | 43 |
| 4 |
0 | 1 | 1 | 1 | 0 | 3 | |
0 | 1 | 0 | 3 | 0 | 4 |
| 5 |
20 | 43 | 8 | 0 | 6 | 77 | |
12 | 96 | 16 | 0 | 149 | 273 |
| Total |
77 | 331 | 67 | 1 | 10 | 486 | |
37 | 245 | 46 | 4 | 268 | 600 |
| Cohort 3 | | | | | | |
| | | | | |
| 1 |
92 | 5 | 0 | 0 | 1 | 98 | |
39 | 7 | 2 | 0 | 15 | 63 |
| 2 |
22 | 329 | 3 | 5 | 7 | 366 | |
14 | 137 | 2 | 1 | 48 | 202 |
| 3 |
2 | 1 | 31 | 0 | 3 | 37 | |
6 | 7 | 11 | 1 | 14 | 39 |
| 4 |
0 | 1 | 0 | 0 | 0 | 1 | |
0 | 1 | 0 | 0 | 0 | 1 |
| 5 |
9 | 7 | 2 | 0 | 4 | 22 | |
34 | 143 | 12 | 2 | 101 | 292 |
| Total |
125 | 343 | 36 | 5 | 15 | 524 | |
93 | 295 | 27 | 4 | 178 | 597 |
| Cohort 4 | | | | | | |
| | | | | |
| 1 |
175 | 10 | 2 | 1 | 1 | 189 | |
79 | 9 | 1 | 0 | 19 | 108 |
| 2 |
48 | 409 | 5 | 15 | 10 | 487 | |
26 | 217 | 4 | 6 | 69 | 322 |
| 3 |
4 | 9 | 22 | 6 | 4 | 45 | |
4 | 6 | 3 | 1 | 16 | 30 |
| 4 |
0 | 5 | 1 | 2 | 0 | 8 | |
1 | 1 | 1 | 6 | 1 | 10 |
| 5 |
8 | 1 | 0 | 0 | 7 | 16 | |
42 | 218 | 16 | 3 | 123 | 402 |
| Total |
235 | 434 | 30 | 24 | 22 | 745 | |
152 | 451 | 25 | 16 | 228 | 872 |
| Cohort 5 | | | | | | |
| | | | | |
| 1 |
102 | 12 | 0 | 5 | 2 | 121 | |
47 | 8 | 0 | 1 | 11 | 67 |
| 2 |
50 | 191 | 3 | 23 | 11 | 278 | |
35 | 111 | 2 | 7 | 50 | 205 |
| 3 |
2 | 5 | 1 | 4 | 2 | 14 | |
9 | 7 | 1 | 0 | 5 | 22 |
| 4 |
1 | 2 | 0 | 2 | 2 | 7 | |
0 | 1 | 0 | 0 | 2 | 3 |
| 5 |
5 | 3 | 0 | 1 | 2 | 11 | |
24 | 102 | 5 | 5 | 58 | 194 |
| Total |
160 | 213 | 4 | 35 | 19 | 431 | |
115 | 229 | 8 | 13 | 126 | 491 |
| Grand total |
634 | 1517 | 196 | 65 | 72 | 2484 | |
420 | 1353 | 150 | 38 | 1106 | 3067 |
Table A.5:
Class, age 25 by age 35, by cohort and sex
| State |
State at 35 |
| | | | | |
| at 25 |
Men |
| Women | | | | | |
| |
1 | 2 | 3 | 4 | 5 | Total | |
1 | 2 | 3 | 4 | 5 | Total |
| Cohort 1 | | | | | | |
| | | | | |
| 1 |
20 | 2 | 2 | 0 | 0 | 24 | |
36 | 3 | 1 | 0 | 0 | 40 |
| 2 |
6 | 22 | 2 | 0 | 0 | 30 | |
1 | 107 | 0 | 0 | 2 | 110 |
| 3 |
0 | 0 | 13 | 0 | 0 | 13 | |
0 | 1 | 11 | 0 | 0 | 12 |
| 4 |
4 | 2 | 2 | 70 | 9 | 87 | |
2 | 3 | 1 | 41 | 3 | 50 |
| 5 |
3 | 2 | 3 | 11 | 58 | 77 | |
1 | 8 | 0 | 5 | 121 | 135 |
| Total |
33 | 28 | 22 | 81 | 67 | 231 | |
40 | 122 | 13 | 46 | 126 | 347 |
| Cohort 2 | | | | | | |
| | | | | |
| 1 |
44 | 0 | 0 | 1 | 1 | 46 | |
56 | 2 | 0 | 1 | 0 | 59 |
| 2 |
7 | 41 | 2 | 3 | 6 | 59 | |
9 | 210 | 1 | 2 | 15 | 237 |
| 3 |
0 | 0 | 30 | 1 | 0 | 31 | |
0 | 0 | 7 | 0 | 0 | 7 |
| 4 |
7 | 2 | 5 | 94 | 8 | 116 | |
0 | 3 | 0 | 36 | 12 | 51 |
| 5 |
8 | 2 | 7 | 12 | 120 | 149 | |
3 | 19 | 1 | 3 | 119 | 145 |
| Total |
66 | 45 | 44 | 111 | 135 | 401 | |
68 | 234 | 9 | 42 | 146 | 499 |
| Cohort 3 | | | | | | |
| | | | | |
| 1 |
96 | 1 | 4 | 1 | 0 | 102 | |
79 | 5 | 1 | 0 | 0 | 85 |
| 2 |
8 | 25 | 2 | 0 | 3 | 38 | |
10 | 195 | 7 | 6 | 18 | 236 |
| 3 |
0 | 0 | 46 | 1 | 1 | 48 | |
0 | 1 | 5 | 0 | 0 | 6 |
| 4 |
9 | 3 | 6 | 124 | 21 | 163 | |
3 | 6 | 4 | 27 | 7 | 47 |
| 5 |
3 | 2 | 13 | 6 | 105 | 129 | |
3 | 14 | 1 | 6 | 100 | 124 |
| Total |
116 | 31 | 71 | 132 | 130 | 480 | |
95 | 221 | 18 | 39 | 125 | 498 |
| Cohort 4 | | | | | | |
| | | | | |
| 1 |
182 | 3 | 4 | 0 | 2 | 191 | |
122 | 10 | 1 | 1 | 4 | 138 |
| 2 |
11 | 51 | 3 | 1 | 4 | 70 | |
27 | 294 | 14 | 8 | 47 | 390 |
| 3 |
1 | 2 | 61 | 2 | 3 | 69 | |
1 | 1 | 20 | 0 | 1 | 23 |
| 4 |
21 | 1 | 13 | 140 | 17 | 192 | |
2 | 7 | 2 | 42 | 12 | 65 |
| 5 |
8 | 2 | 19 | 20 | 123 | 172 | |
4 | 24 | 6 | 5 | 113 | 152 |
| Total |
223 | 59 | 100 | 163 | 149 | 694 | |
156 | 336 | 43 | 56 | 177 | 768 |
| Cohort 5 | | | | | | |
| | | | | |
| 1 |
207 | 5 | 6 | 2 | 3 | 223 | |
141 | 10 | 5 | 3 | 6 | 165 |
| 2 |
31 | 38 | 5 | 5 | 4 | 83 | |
52 | 279 | 19 | 7 | 38 | 395 |
| 3 |
2 | 1 | 59 | 4 | 4 | 70 | |
1 | 2 | 5 | 0 | 1 | 9 |
| 4 |
27 | 4 | 19 | 163 | 19 | 232 | |
1 | 4 | 4 | 27 | 9 | 45 |
| 5 |
11 | 5 | 16 | 16 | 105 | 153 | |
4 | 30 | 7 | 12 | 108 | 161 |
| Total |
278 | 53 | 105 | 190 | 135 | 761 | |
199 | 325 | 40 | 49 | 162 | 775 |
| Grand total |
716 | 216 | 342 | 677 | 616 | 2567 | |
558 | 1238 | 123 | 232 | 736 | 2887 |
Table A.6:
Class, age 25 by age 40, by cohort and sex
| State |
State at 40 |
| | | | | |
| at 25 |
Men |
| Women | | | | | |
| |
1 | 2 | 3 | 4 | 5 | Total | |
1 | 2 | 3 | 4 | 5 | Total |
| Cohort 1 | | | | | | |
| | | | | |
| 1 |
20 | 2 | 2 | 0 | 0 | 24 | |
34 | 4 | 2 | 0 | 0 | 40 |
| 2 |
6 | 22 | 2 | 0 | 0 | 30 | |
2 | 103 | 0 | 1 | 4 | 110 |
| 3 |
0 | 0 | 13 | 0 | 0 | 13 | |
0 | 1 | 11 | 0 | 0 | 12 |
| 4 |
5 | 2 | 3 | 65 | 12 | 87 | |
4 | 4 | 1 | 35 | 6 | 50 |
| 5 |
4 | 4 | 5 | 14 | 50 | 77 | |
1 | 10 | 1 | 4 | 119 | 135 |
| Total |
35 | 30 | 25 | 79 | 62 | 231 | |
41 | 122 | 15 | 40 | 129 | 347 |
| Cohort 2 | | | | | | |
| | | | | |
| 1 |
42 | 1 | 1 | 2 | 0 | 46 | |
55 | 2 | 0 | 0 | 2 | 59 |
| 2 |
10 | 36 | 3 | 3 | 7 | 59 | |
11 | 194 | 5 | 6 | 21 | 237 |
| 3 |
0 | 1 | 29 | 1 | 0 | 31 | |
0 | 1 | 5 | 0 | 1 | 7 |
| 4 |
7 | 4 | 4 | 91 | 10 | 116 | |
0 | 4 | 2 | 28 | 17 | 51 |
| 5 |
8 | 3 | 7 | 11 | 120 | 149 | |
4 | 23 | 1 | 7 | 110 | 145 |
| Total |
67 | 45 | 44 | 108 | 137 | 401 | |
70 | 224 | 13 | 41 | 151 | 499 |
| Cohort 3 | | | | | | |
| | | | | |
| 1 |
97 | 1 | 2 | 2 | 0 | 102 | |
72 | 9 | 2 | 0 | 2 | 85 |
| 2 |
9 | 23 | 3 | 0 | 3 | 38 | |
23 | 176 | 7 | 6 | 24 | 236 |
| 3 |
0 | 0 | 46 | 1 | 1 | 48 | |
0 | 1 | 5 | 0 | 0 | 6 |
| 4 |
16 | 3 | 8 | 116 | 20 | 163 | |
3 | 7 | 4 | 23 | 10 | 47 |
| 5 |
4 | 2 | 13 | 11 | 99 | 129 | |
7 | 21 | 2 | 9 | 85 | 124 |
| Total |
126 | 29 | 72 | 130 | 123 | 480 | |
105 | 214 | 20 | 38 | 121 | 498 |
| Cohort 4 | | | | | | |
| | | | | |
| 1 |
178 | 7 | 3 | 1 | 2 | 191 | |
116 | 11 | 4 | 1 | 6 | 138 |
| 2 |
18 | 43 | 2 | 2 | 5 | 70 | |
48 | 261 | 14 | 12 | 55 | 390 |
| 3 |
3 | 2 | 59 | 3 | 2 | 69 | |
1 | 1 | 19 | 0 | 2 | 23 |
| 4 |
23 | 0 | 18 | 134 | 17 | 192 | |
3 | 8 | 2 | 38 | 14 | 65 |
| 5 |
11 | 3 | 18 | 23 | 117 | 172 | |
5 | 28 | 7 | 7 | 105 | 152 |
| Total |
233 | 55 | 100 | 163 | 143 | 694 | |
173 | 309 | 46 | 58 | 182 | 768 |
| Cohort 5 | | | | | | |
| | | | | |
| 1 |
113 | 1 | 4 | 4 | 2 | 124 | |
65 | 6 | 3 | 0 | 4 | 78 |
| 2 |
22 | 12 | 5 | 5 | 1 | 45 | |
48 | 142 | 10 | 15 | 30 | 245 |
| 3 |
1 | 1 | 29 | 4 | 1 | 36 | |
1 | 0 | 2 | 1 | 2 | 6 |
| 4 |
26 | 3 | 11 | 78 | 11 | 129 | |
0 | 4 | 2 | 17 | 4 | 27 |
| 5 |
12 | 3 | 11 | 11 | 45 | 82 | |
7 | 15 | 6 | 7 | 50 | 85 |
| Total |
174 | 20 | 60 | 102 | 60 | 416 | |
121 | 167 | 23 | 40 | 90 | 441 |
| Grand Total |
635 | 179 | 301 | 582 | 525 | 2222 | |
510 | 1036 | 117 | 217 | 673 | 2553 |

 Copyright Sociological Research Online, 1999
Copyright Sociological Research Online, 1999

 Abstract
Abstract Introduction
Introduction Class as a Contested Concept
Class as a Contested Concept Class as a Longitudinal Concept
Class as a Longitudinal Concept Class versus 'General Status'
Class versus 'General Status' Data and Method
Data and Method Bias
Bias The Method
The Method Descriptives
Descriptives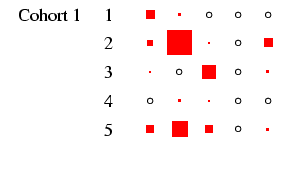

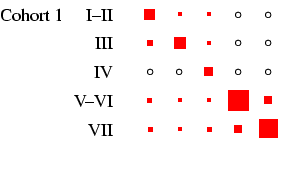

 Models
Models Results: General status to age 35
Results: General status to age 35 Class to age 35
Class to age 35 Mobility to age 40
Mobility to age 40 Reviewing the results: the direction and magnitude of
change
Reviewing the results: the direction and magnitude of
change Discussion
Discussion![]()
 Notes
Notes![]()
 Appendix
Appendix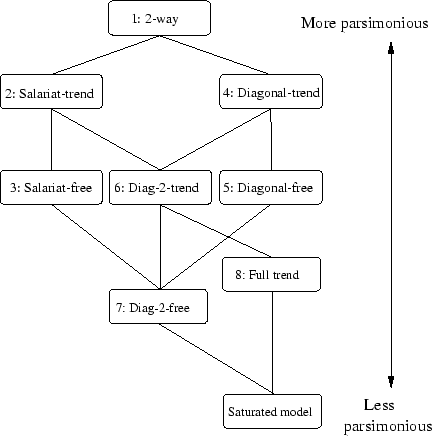
![]()
![]()
![]() is equal to 1 unless status at 25 and
status at 35 are both salariat and is otherwise to be estimated,
with
is equal to 1 unless status at 25 and
status at 35 are both salariat and is otherwise to be estimated,
with ![]() being raised to the power of k, the index of
cohort.
being raised to the power of k, the index of
cohort.
![]()
![]() is equal to 1 unless status at 25 and
status at 35 are both salariat and is otherwise to be estimated,
with
is equal to 1 unless status at 25 and
status at 35 are both salariat and is otherwise to be estimated,
with
![]() having independent values for each cohort.
having independent values for each cohort.
![]()
![]() is equal to 1 unless i = j, in which case it is
to be estimated.
is equal to 1 unless i = j, in which case it is
to be estimated.
![]()
![]() is equal to 1 unless i = j, in which case it is
to be estimated.
is equal to 1 unless i = j, in which case it is
to be estimated.
![]()
![]() is equal to 1 unless i = j, and is otherwise to
be estimated. (
is equal to 1 unless i = j, and is otherwise to
be estimated. (![]() is
equivalent to
is
equivalent to ![]() given this condition; the choice of
subscript is arbitrary.)
given this condition; the choice of
subscript is arbitrary.) ![]() is raised to the power of
k, the index of cohort.
is raised to the power of
k, the index of cohort.
![]()
![]() is equal to 1 unless i = j, and is otherwise to
be estimated. (
is equal to 1 unless i = j, and is otherwise to
be estimated. (![]() is
equivalent to
is
equivalent to ![]() given this condition; the choice of
subscript is arbitrary.)
given this condition; the choice of
subscript is arbitrary.)
![]()
![]() is a term for each element of the status
at 25/at 35 association, raised to the power of k.
is a term for each element of the status
at 25/at 35 association, raised to the power of k.
![]()
![]() ,
and has no degrees of freedom.
,
and has no degrees of freedom.
![]() (see, e.g.,
Bishop et al. 1975, pp. 524ff). Where models are not nested, as,
for instance, models 7 and 8,
this relationship does not hold, and insofar as we examine their
difference in fit in these terms it can only be illustrative.
Model 8 is both more general than
model 7, in that it allows change in the
off-diagonal association, and less, in that it restricts the
change in diagonal association to be log-linear (i.e., proportional).
It is, however, slightly more parsimonious.
(see, e.g.,
Bishop et al. 1975, pp. 524ff). Where models are not nested, as,
for instance, models 7 and 8,
this relationship does not hold, and insofar as we examine their
difference in fit in these terms it can only be illustrative.
Model 8 is both more general than
model 7, in that it allows change in the
off-diagonal association, and less, in that it restricts the
change in diagonal association to be log-linear (i.e., proportional).
It is, however, slightly more parsimonious.
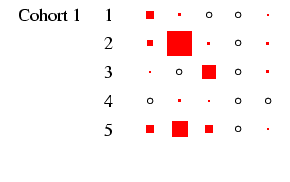

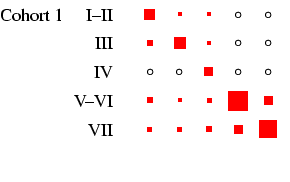

![]()
![]() Copyright Sociological Research Online, 1999
Copyright Sociological Research Online, 1999